Gitterpunkte auf dem Rand einer Ellipse bzw. des Kreises

1. Die Funktion  z = x² + xy + y² stellt das elliptische Paraboloid dar.

2. Die einfachere Form  z = x² + y² stellt das Dreharaboloid dar.

Beide Funktionen nehmen nur positive z-Werte an (mit Ausnahme von x=0 und y=0).
Sind die beide Variablen x und y ganzzahlig, dann ist z eine natürliche Zahl. Aber nicht jede beliebige natürliche Zahl, z. B. nicht z=6. 
Interessant ist die Gleichungen z = x² + xy + y und z = x² + y²  als s. g. diophantische Gleichungen mit ganzzahligen Lösungen zu betrachten.

Für jede z-Wert erhalten wir ein waagerechter Schnitt des Paraboloids, der eine Ellipse bzw. ein Kreis darstellt.
Bei ganzzaligen Lösungen haben wir mit Ellipsen und Kreisen, die durch Gitterpunkte gehen, zu tun.

Beispiele:

Ellipse

1.1  Ellipse z = x² + xy + y² = 301

Diese Ellipse geht durch 24 Gitterpunkte.

Bemerkung:

Wenn (m, n) ein ganzzahliges Lösungspaar der Gleichung x² + xy + y² = k darstellt, dann auch elf weitere Paare, und zwar:
(-m, -n), (n, m), (-n, -m), (m, -m-n), (-m, m+n), (n, -m-n), (-n, m+n), (m+n, m),  (-m-n, -m), (m+n, n),  (-m-n, -n)  ganzzahlige Lösungen sind.

Für k = 301 haben wir zwei primäre Lösungspaare: (4, 15) und  (9, 11).

Kreise

Interessan sind vor allem die Fälle für z = c², wo c eine natürliche Zahl ist. Dann haben wir mit pythagoreischen Tripel zu tun.

2.1  Kreis z = x² + y² = 5² = 25

2.2  Kreis z = x² + y² = 25² = 625

2.3  Kreis z = x² + y² = 65² = 4225

Dieser Kreis geht durch 36 Gitterpunkte. Drei davon sind primitive pythagoreische Tripel: (16, 63, 65), (33, 56, 65) und (39, 52, 65).

2.4  Kreis z = x² + y² = 85² = 7225

Dieser Kreis geht durch 36 Gitterpunkte. Drei davon sind primitive pythagoreische Tripel: (13, 84, 85), (36, 77, 85) und (51, 68, 85).

2.5  Kreis z = x² + y² = 325² = 105625

Dieser Kreis geht durch 60 Gitterpunkte. Drei davon sind primitive pythagoreische Tripel: (36, 323, 325), (91, 312, 325) und (204, 253, 325).

2.6  Kreis z = x² + y² = 425² = 180625

Auch dieser Kreis geht durch 60 Gitterpunkte. Drei davon sind primitive pythagoreische Tripel: (87, 416, 425), (115, 408, 425) und (297, 304, 425).

Man kann das Problem in die dritte Dimension übertragen. Nah ist die Frage: wie viele Gitterpunkte liegen auf der Oberfläche der Kugel (Sphäre) mit dem radius R=325 bzw. R=425? 
Beispiele als o2c-Objekte: auf der Oberfläche der Kugel mit dem Radius R=25 liegen 150 Gitterpunkte, mit dem Radius R=33 390 Gitterpunkte (Bild unten), mit dem Radius R=51 486 Gitterpunkte.

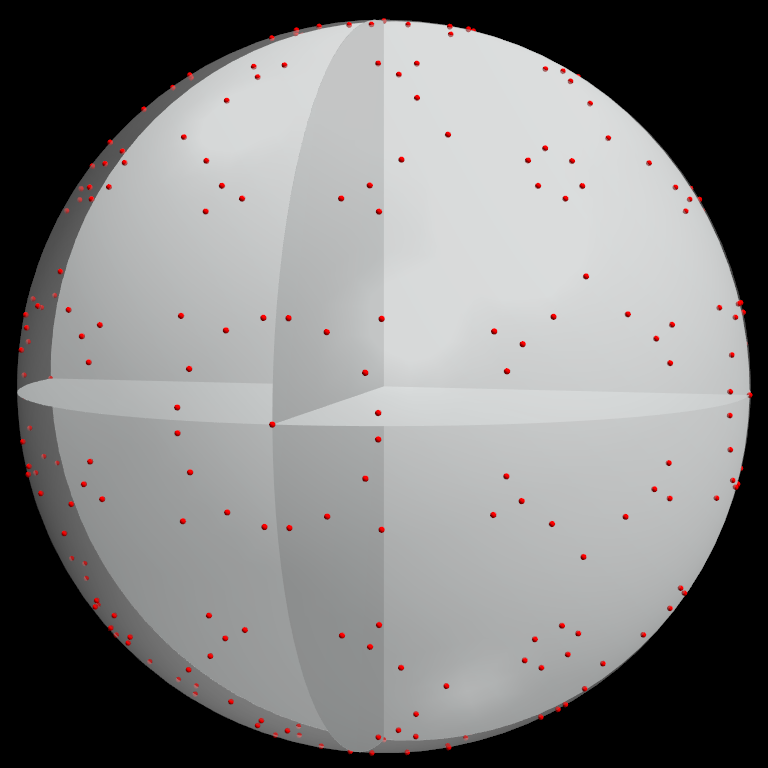
Gitterpunkte auf der Oberfläche der Kugel mit dem Radius R=33

Einige Punkte sind koplanar und sie bilden Ecken eines interessantes Polyeders mit 572 Facetten:

Gitterpunkte auf bekannten, symmetrischen Formen:

Bemerkung

Die Funktion  z = x² + kxy + y² stellt eine Quadrik dar, die vom Parameter k abhängig ist.

Für k = 0 ist es eine Kugel,
für  0 < k < 2 ist es ein elliptisches Paraboloid,
für k = 2 ist es ein parabolischer Zylinder und
für k > 2 ist es ein hyperbolisches Paraboloid.

Nebenbei:

3² + 4² = 5²
33² + 44² = 55²
333² + 444² = 555²

und so weiter. 

Stand: 09.06. 2020

Erstellt: 15.08. 2013

© Tadeusz E. Dorozinski