Aksonometria prostokątna

Aksonometria prostokątnana lepiej odwzorowywuje przestrzeń niż aksonometria ukośna i dlatego powinna być jak najczęściej stosowana.
Podobnie jak w rzutowaniu prostokątnym (normalnym) na dwie lub na trzy rzutnie, rzutujemy w niej objekty przestrzenne prostopadle, ale tylko na jedną rzutnie

Przez odpowiednie obracanie obiektu trójwymiarowego możemy w rzutach prostokątnych otrzymać jego owzorowanie aksonometryczne.
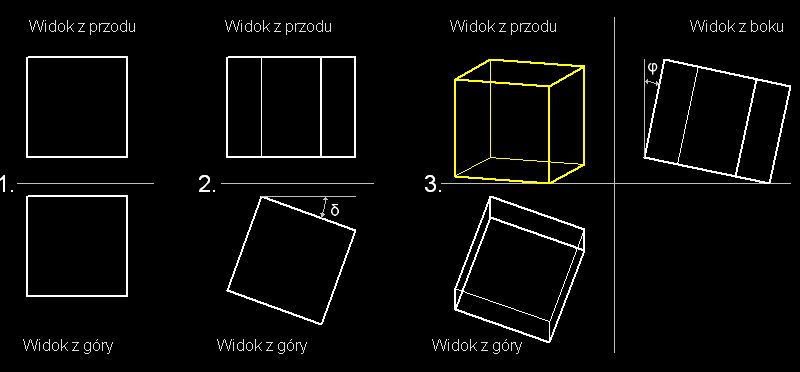
Poniżej (rys. 1) przykład z sześcianem:

Rys. 1

Najpierw mamy sześcian w położeniu normalnym (1. faza).
W drugiej fazie obracamy sześcian wokół osi pionowej o pewien kąt δ.
W trzeciej fazie pochylamy sześcian do przodu o pewien kąt φ (obrót wokół pewnej osi poziomej równoległej do osi X).
W ten sposób uzyskujemy widok sześcianu, gdzie pionowe krawędzie sześcianu odwzorowane są jako linie pionowe.
Ten widok (na rys. 1 w kolorze żółtym) możemy traktować więc jako obraz sześcianu w aksonometrii prostokątnej
Uwaga: zamiana kojejności obrotów prowadzi do innych, niepożądanych rezultatów.

Na tab. I przedstawione są różne położenia sześcianu. Kąty δ i φ przyjmują wartości od 0° do 90° co 5°.

Tab. I

Tu tablica l  w wielkości 2024*2024 pixeli w formacie PNG i w wersji linearnej.

Bryły obrotowe o pionowej osi są w aksonometrii prostokątnej poprawnie odwzorowywane.

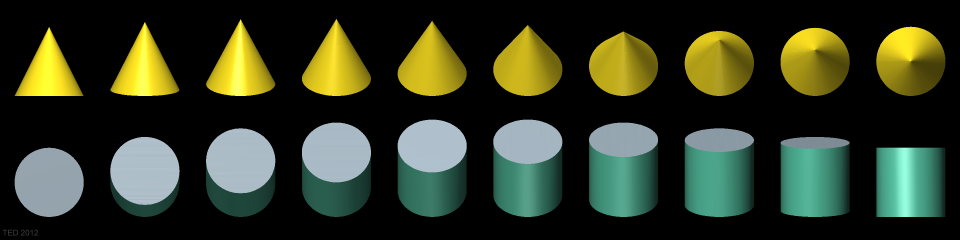
Tab. II

Konstrukcja

Wykonywanie rysunków aksonometrycznych za pośrednictwem rzutów prostokątnych jest dość uciążliwe. Metoda bezpośrednia jest szybsza i wygodniejsza. 

W roku 1975 na Politechnice Wrocławskiej opublikowałem pracę "Nowy sposób wyznaczania parametrów aksonometrii prostokątnej".
Opisaną tam innowacyjną metodę, którą nazwijmy 'metodą Doro', przedstawiam w skrócie tutaj.
Metoda ta jest prostsza i wygodniejsza niż podręcznikowa metoda z trójkątem śladów, która ma cechy przypadkowości.

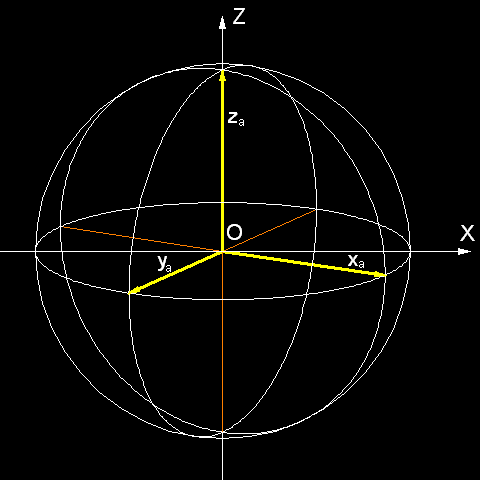
Na rys. 2 mamy projekcję kuli jednostkowej (promień = e = 1) na płaszczyznę XZ, a na rys. 3 dwa rzuty prostopadłe tej kuli.
Wychodzące ze środka kuli trzy osie aksonometryczne odpowiadają pewnym trzem wzajemnie prostopadłym osiom x, y i z, które zostały obrócone o kąty δ i φ.
Poziome osie x i y leżą w plaszczyźnie równikowej kuli, a oś z przechodzi przez jej biegun północny N. Równik kuli widoczny jest jako elipsa.

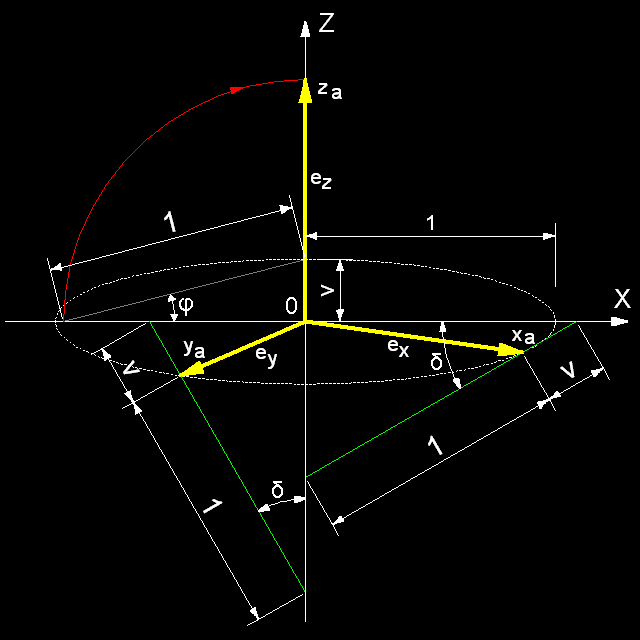
Rys. 2

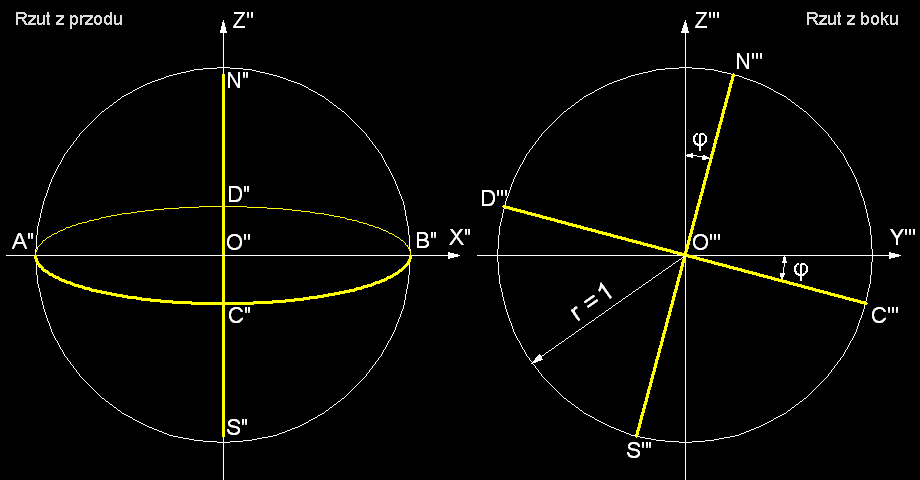
Rys. 3

Z powyższych rysunków wynika:
półosie wielkie elipsy A''O'' = B''O'' = 1
półosie małe elipsy C''O'' = D''O'' = sin φ = v
Oś pionową widzimy w skrócie; mamy przy tym O''N'' = cos φ 

Położenie osi aksonometrycznych x_a und y_a zależy od kąta obrotu δ, ale zawsze stanowią one parę osi sprzężonych elipsy.
Do wyznaczenia ich wykorzystujemy pewną własność metody papierkowej wyznaczania punktów na elipsie

Dwa wzajemnie prostopadłe położenia paska papieru określają punkty dwóch osi sprzężonych elipsy (Rys. 4).

Rys. 4

Rys. 4 jest kwintensencją mojej metody.
Zielone odcinki przedstawiają symbolicznie skrawek papieru w dwóch wzajemnie prostopadłych położeniach, przy czym ich nachylenie odpowiednio do osi X i Y wynosi δ (sic!).

Wszystkie parametery aksonometrii prostokątnej można obliczyć także rachunkowo (rys. 5).

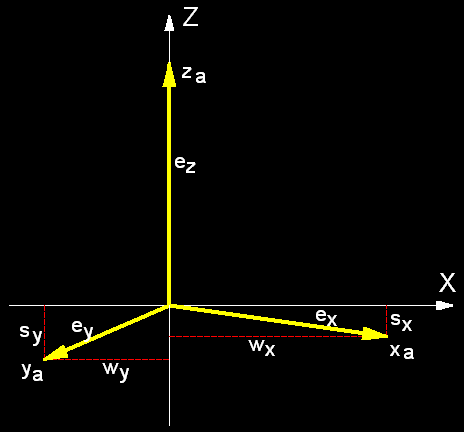
Rys. 5

Parametery aksonometrii:  

Mamy dane: kąt obrotu δ  i kąt pochylenia φ.

Wówczas:
 v = sin  φ

Koordynaty poziome:
w_x = cos δ 
w_y = sin δ 

Koordynaty pionowe i skróty:
s_x = sin δ  * sin φ  = v * sin δ
s_y = cos δ  * sin φ = v  * cos δ
e_x = SQRT (cos² δ + v² * sin² δ)
e_y = SQRT (sin² δ + v² * cos² δ)
e_z = cos φ

Uwaga: SQRT oznacza pierwiastek kwadratowy

Znana jest następująca równość:

e_x² + e_y² + e_z²  = 2 

Uwaga

Jeśli ktoś chciałby korzystać dodatkowo z kostrukcji opartych na tzw. trójkącie śladów aksonometrycznych, to może dorysować dowolnie wielki trójkąt, ktąrego boki są prostopadłe do osi x_a, y_a i z_a.

Izometria

Znana i popularna jest izometria. Jest to szczególny przypadek aksonometrii prostokątnej. 
W przypadku izometrii kąty między osiami aksonometrycznymi x_a, y_a i z_a są jednakowe i wynoszą 120° (Rys. 6).
Również skróty są jednakowe (e_x = e_y = e_z = 0,8165). W praktyce przyjmuje się je za 1, czyli obiekty przestrzenne rysowane są nieco powiększone (122,5%).

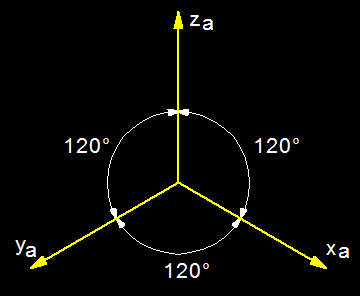
Rys. 6

Według mojej metody kąty δ und φ w przypadku izometrii wynoszą odpowiednio 45° oraz 35,2644° (35°15' 52").

Przypis

Skróty aksonometryczne mają duże znaczenie, gdyż decydująco wpływają na spostrzeganie i na rozpoznawanie obiektów na rysunkach aksonometrycznych.
Zabawnym potwierdzeniem tego jest przykład iluzji optycznej Rogera N. Sheparda z dwoma stołami:

Widzimy na obrazku dwa stoły, z których ten po lewj stronie wydaje sie być węższym niż prawy.
Z niedowierzaniem przyjmujemy fakt, że oba blaty stołów mają na rysunku ten sam kształt i wielkość! Proszę kliknąć na grafikę w celu sprawdzenia tego.

© Tadeusz E. Dorozinski

Kontakt

Stand: 15.11.2012

Startseite