Normale Axonometrie

Normale Axonometrie wirkt anschaulicher als allgemeine (schiefe) Axonometrie und deswegen sollte sie immer  bevorzugt werden.
Man nennt sie auch orthogonale bzw. senkrechte Axonometrie.

In Zwei- bzw. Dreitafelprojektion werden räumliche Objekte senkrecht auf Bildebenen projiziert. Man  kann also mit diesem Verfahren auch  axonometrische Bilder erzeugen.
Man muss nur das Objekt entsprechend drehen.
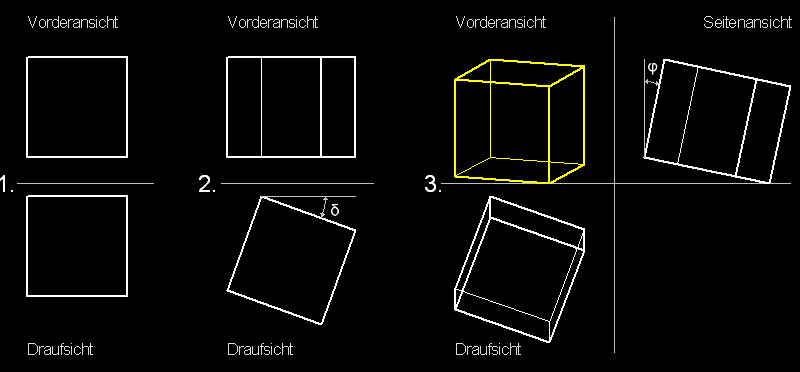
Hier ein Beispiel mit einem Würfel (Abb. 1):

Abb. 1

Zuerst befindet sich der Würfel in einer normalen Lage (1).
In zweitem Schritt wird er um eine senkrechte Achse um einen Winkel δ gedreht.
Im nächstem Schritt kippen wir den Würfel um einen Winkel φ (drehen um eine waagerechte Achse).
So erreichen wir, dass in der Vorderansicht die senkrechte Kanten des Würfels als senkrechte Linien abgebildet sind.
Hinweis: vertauschen wir die Drehungen, dann werden sie nicht senkrecht abgebildet.
In der Vorderansicht im 3. Schritt erhalten wir das normalaxonometrische Bild des Würfels (gelb). 

In der Tafel I sind Würfel in verschiedenen Lagen dargestellt. Die Winkeln δ und φ nehmen die Werte im Bereich von -90° bis 90° in 10° Schritten.

Tafel I

Hier die Tafel  in der Größe 2024*2024  im PNG-Format und schwarz-weiß, linear.

Tafel II

Die Drehkörper mit der senkrechter Drehachse werden in der normalen Axonometrie korrekt dargestellt. Der Drehwinkel spielt dabei keine Rolle.

Tafel III

Konstruktion

Das Zeichnen der normalaxonometrischen Bilder mittels Dreitafelprojektion ist umständlich. Direkte Methoden sind schneller und bequemer.
Hier stelle ich die innovative Doro-Methode vor, die ich bereits vor Jahren in einem Wissenschaftlichen Heft der Technischen Hochschule zu Breslau (Wroclaw) publiziert habe.
Diese Methode ist einfacher und  bequemer als das Einschneideverfahren, vor allem dadurch, dass die nicht "zufällig" sei.

In Abb. 2 befindet sich das Achsenkreuz in der Einheitskugel. Axonometrischen Achsen x und y liegen auf dem Äquatorskreis, der wir im Allgemeinfall als eine Ellipse sehen.
Diese Einheitskugel ist in Abb. 3 in zwei Ansichten dargestellt.
Da kann man folgendes erkennen:

Die Halbachse A''O'' = B''O'' = 1
Die Halbachse C''O'' = D''O'' = sin φ = v
Senkrechte Achse sehen wir verkürzt; dabei ist O''N'' = cos φ .

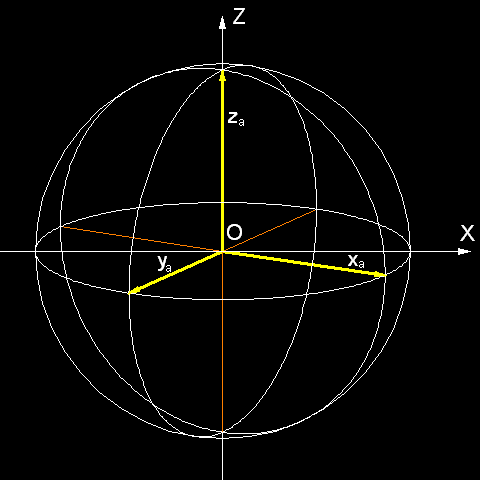
Abb. 2

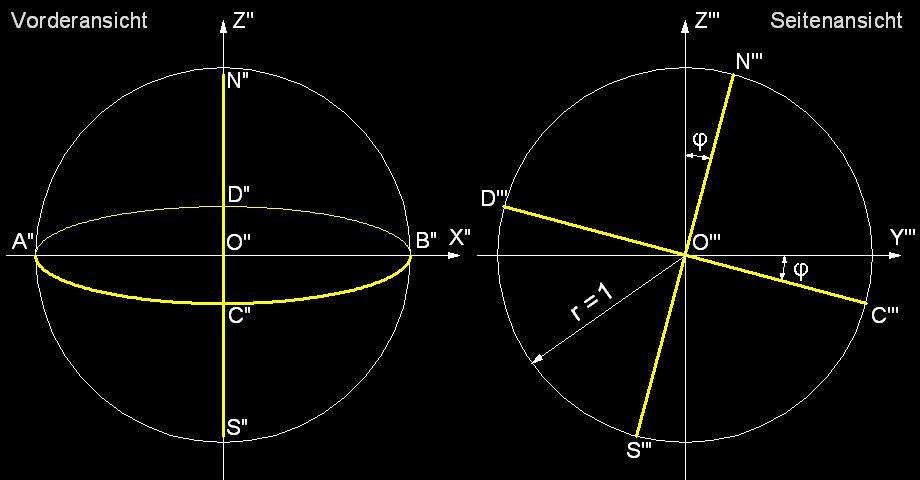
Abb. 3

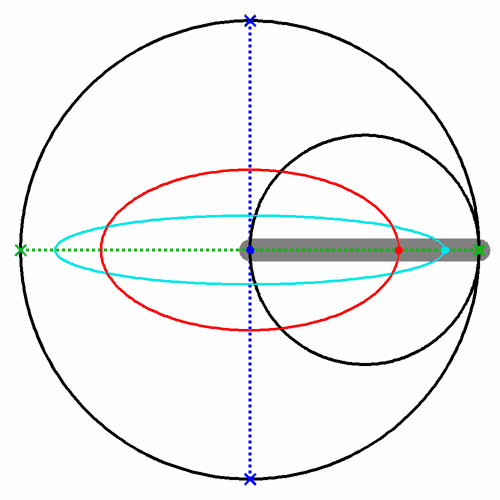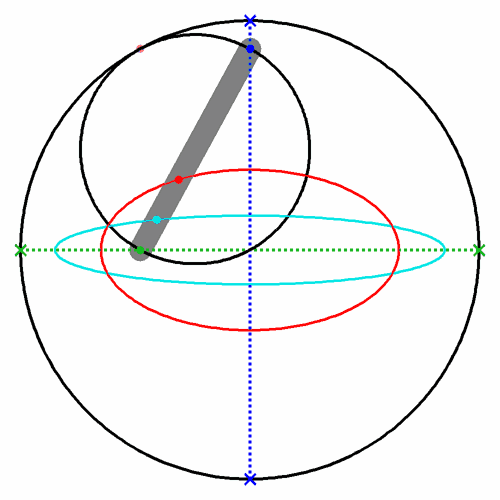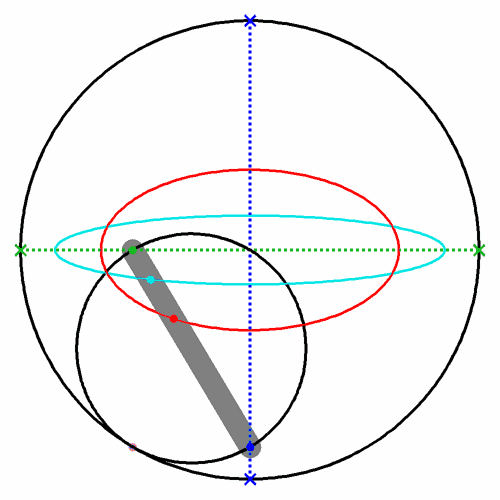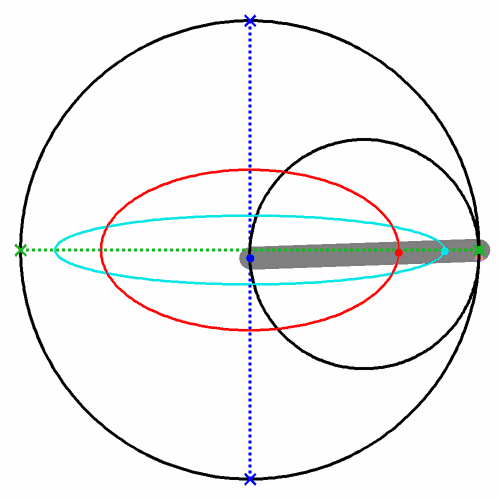
Die Lage der Axonometrieachsen x_a und y_a hängt vom Drehwinkel δ ab. Es ist immer ein Paar der konjugierten Durchmessern der Ellipse. Um die zu bestimmen nutzen wir eine Eigenschaft der Papierstreifenkonstruktion der Ellipse.

Zwei zueinander senkrechte Lagen des Papierstreifens markiere die Endpunkte von zwei konjugierten Durchmessern (Abb. 4).

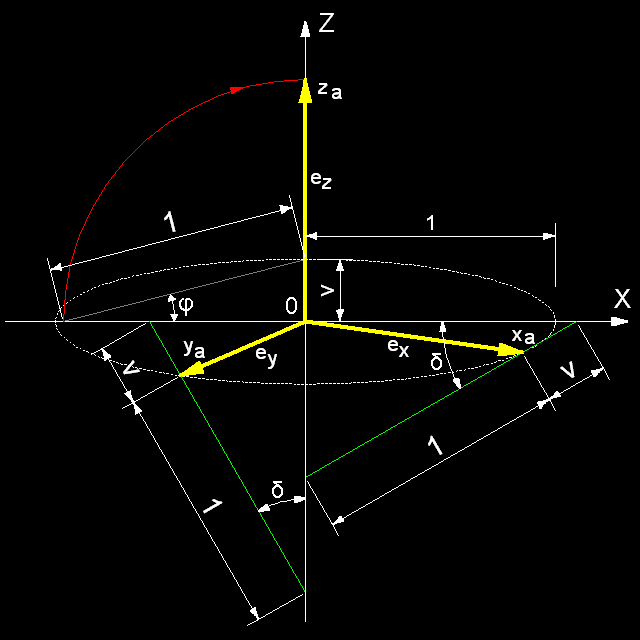
Abb. 4

Die grüne Strecken stellen den Papierstreifenrand dar, dessen entsprechenden Winkel zu Weltachsen X und Z  in beiden Lagen dem Drehwinkel δ gleicht (sic!).
In Abb. 4 ist die ganze Doro-Methode dargestellt, wobei die Ellipse nicht notwendig ist.

Man kann auch alle Parameter der normalen Axonometrie rechnerisch ermitteln. Die sind in Abb. 5 abgebildet.

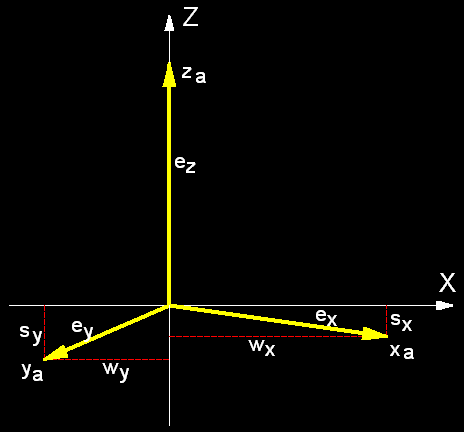
Abb. 5

Alle Parameter:  

Vorgegeben: Drehwinkel δ  und  Kippwinkel φ

Dann
 v = sin  φ

waagerechte Koordinaten:
w_x = cos δ 
w_y = sin δ 

senkrechte Koordinaten und Verkürzungen:
s_x = sin δ  * sin φ  = v * sin δ
s_y = cos δ  * sin φ = v  * cos δ
e_x = SQRT (cos² δ + v² * sin² δ)
e_y = SQRT (sin² δ + v² * cos² δ)
e_z = cos φ

Achtung: SQRT bedeutet Quadratwurzel.

Bekannt ist die folgende Gleichung:

e_x² + e_y² + e_z²  = 2 

Achtung

Wenn man hier zusätzlich die Einschneidenmethode anwenden will, dann muß man lediglich ein beliebig großes Dreieck zeichnen, dessen Seiten senkrecht zu Achsen x_a, y_a und z_a verlaufen.

 Auf Wikimedia gefunden (Autor: Jahobr)

Isometrie

Bekannt und populär ist die Isometrie. Das ist ein Sonderfall der normalen Axonometrie. 
Bei der Isometrie die drei Winkeln zwischen den Axonometrieachsen x_a, y_a und z_a sind gleich. Alle betragen 120° (Abb. 6).
Auch alle Verkürzungen sind gleich (e_x = e_y = e_z = 0,8165). In der Praxis werden die als 1 angenommen, was bedeutet, dass alles etwas vergrößert (122,5%) gezeichnet wird.

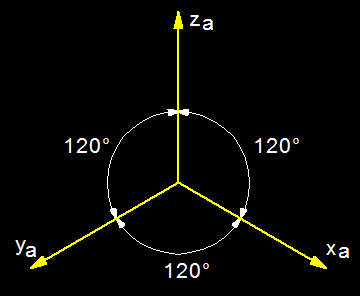
Abb. 6

Nach der Doro-Methode betragen die Winkeln δ und φ im Falle der Isometrie entsprechend 45° und 35,2644° (35°15' 52").

Bemerkung

Verkürzungen spielen sehr wichtige Rolle in der Axonometrie, weil die direkten Einfluss auf das Prozess des Erkennens der Objekte in der Zeichnung haben.
Ein witziger Beispiel dafür ist eine von vielen optischen Täuschungen von Roger N. Shepard und zwar die mit zwei Tischen:

Wir erkennen auf dem Bild zwei Tische. Der linke erscheint uns schmäler als der rechte.
Es ist schwer wahrzunehmen, dass die beide Tischplatten auf dem Bild gleichgroß sind! Bitte aufs Bild klicken!

© Tadeusz E. Dorozinski

Kontakt

Stand: 21.11.2022

Erstellt 2004

Startseite