Reguläre Kugelpackungen
Sphere Packing

Unter der Dichte d einer Kugelpackung versteht man das Verhältnis des von Kugeln gefüllten Volumens zum Gesamtvolumen.

k = Anzahl der Kontakte mit Nachbarnkugeln (Kontaktzahl).

Hinweise zu o2c-Objekten hier.

1. Steife reguläre Kugelpackungen

1.1. Kugelpackungen mit dem Primärnetz Netz 4

k = 4   Dichte d = 0,3401    o2c-Objekt

k = 6   Dichte d = 0,3702 

1.2. Kugelpackungen mit dem Primärnetz Netz 6

k = 6   Dichte d = 0,5236 

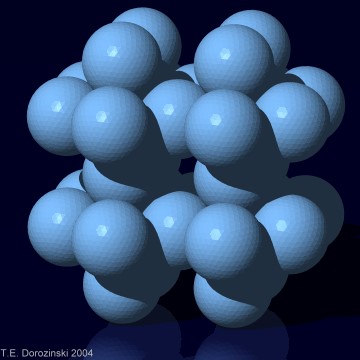
k = 8   Dichte d = 0,5554

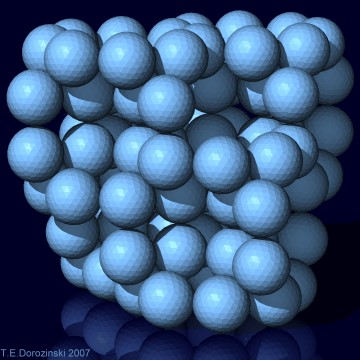
k = 6   Dichte d = 0,4210 

k = 5   Dichte d = 0,3081  Schema als o2c-Objekt

k = 6   Dichte d =?

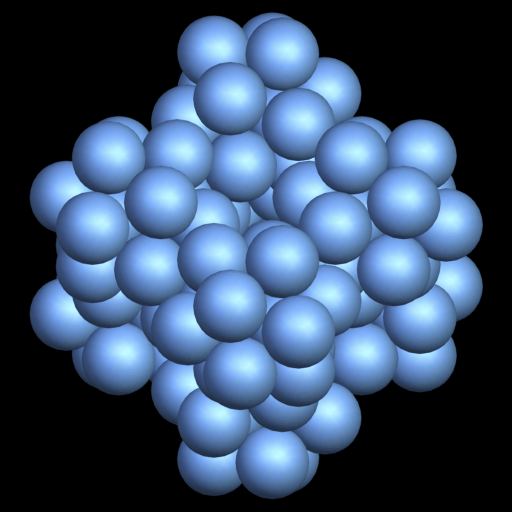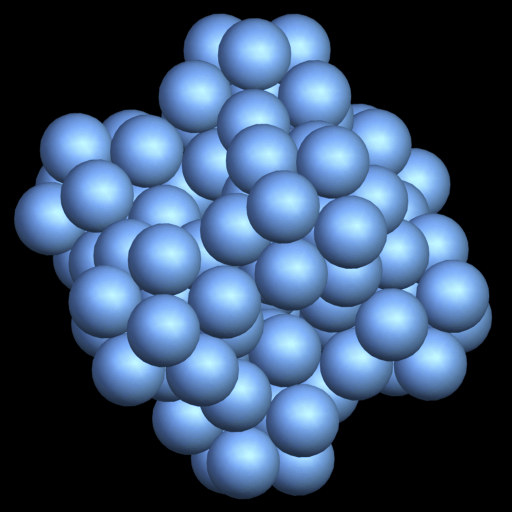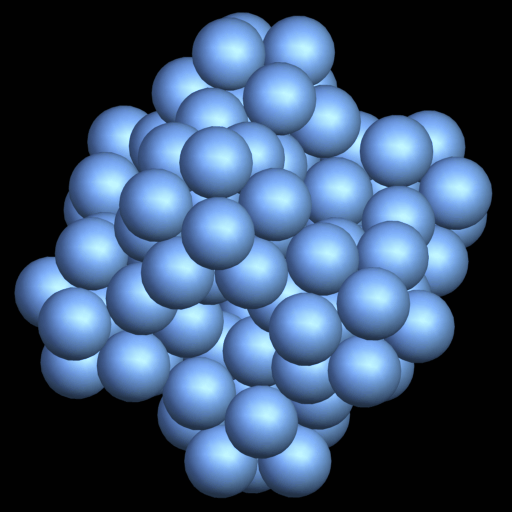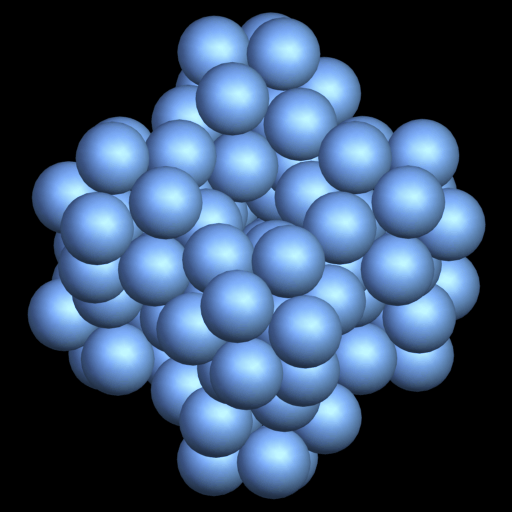
k = 7   Dichte d =?, nicht steif!  Schema

1.3. Kugelpackungen mit dem Primärnetz Netz 8

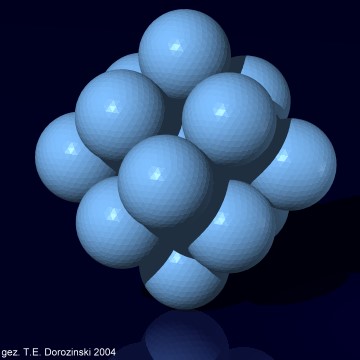
k = 8   Dichte d = 0,6802

1.4. Kugelpackungen mit dem Primärnetz Netz 12

 
k = 12   Dichte d = 0,7405 

1.5. Steife halbreguläre Kugelpackung

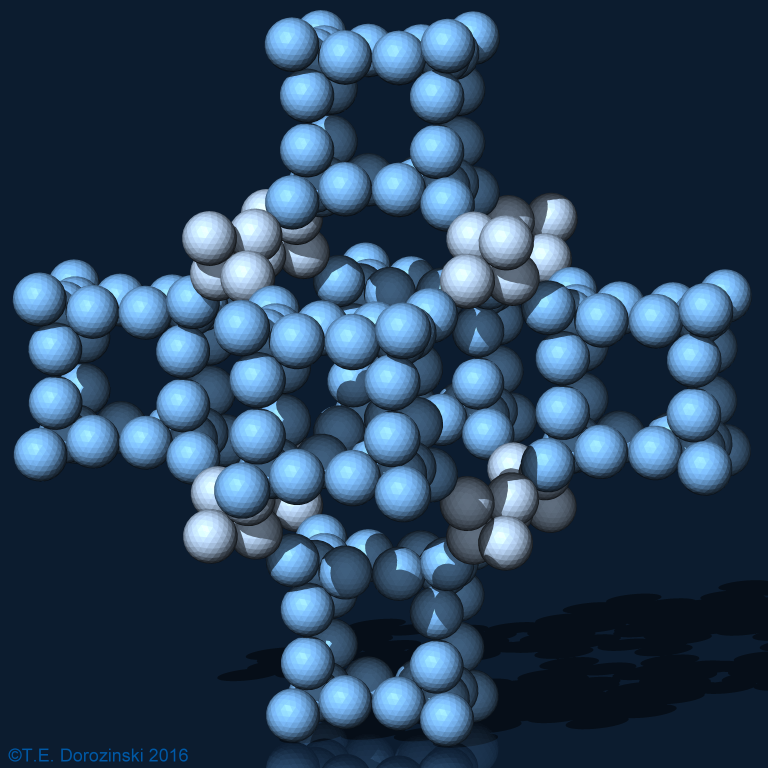
k = 4   Dichte d = 0,09786   Schema als o2c-Objekt

2. Lose reguläre Kugelpackungen

   
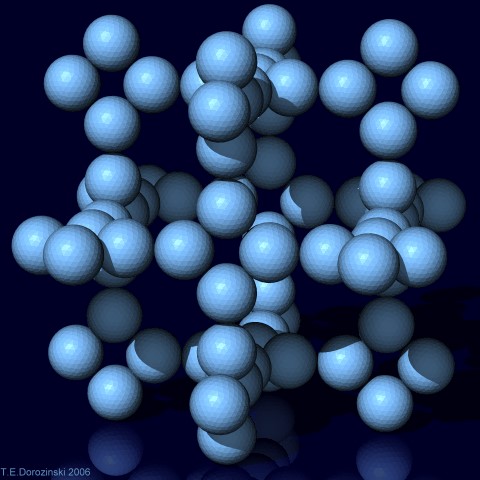
k = 3   Dichte d = 0,11163    

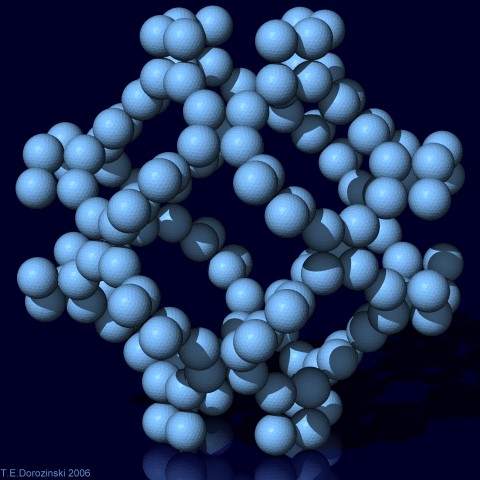
k = 3   Dichte d = 0,08815    Auch als o2c-Objekt

k = 3   Dichte d = 0,3291 

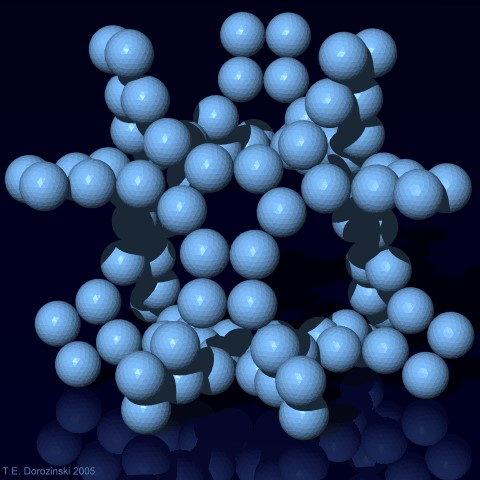
k = 3   Dichte d = 0,083858  

k = 3   Dichte d = 0,09853  

k = 3   Dichte  d = 0,0555      Die Heesch-Laves-Packung. 

k = 3   Dichte d = 0,034575

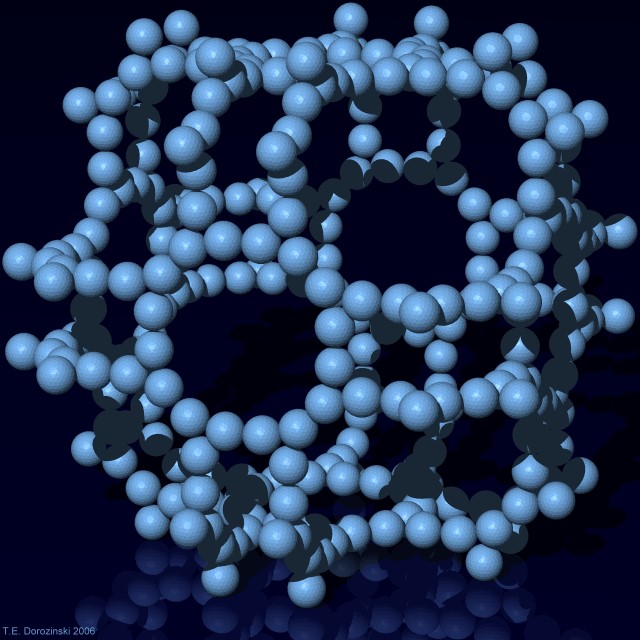
k = 3   Dichte d = 0,036673   

Zurück

3. Schichtweise aufgebaute Kugelpackungen

Es handelt sich um Kugelpackungen, die von regelmäßigen 2D-Netzen abgeleitet werden.

3.1.   2D-Netz (3, 12, 12) 

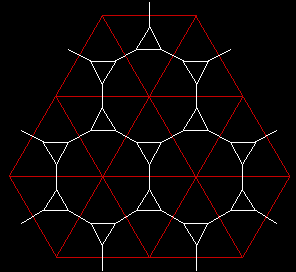
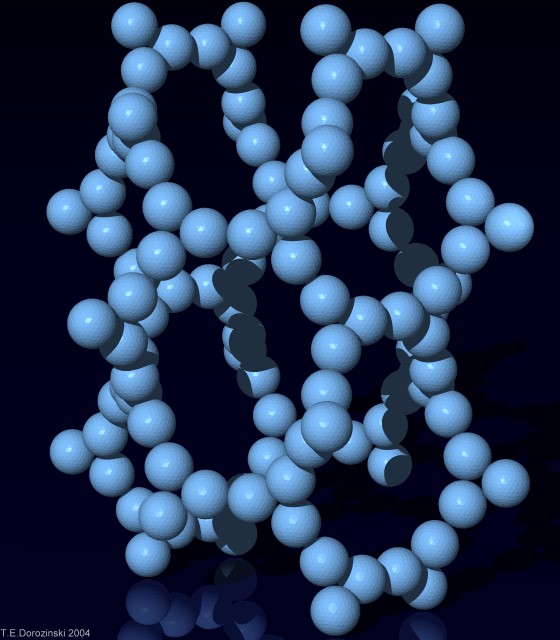
k = 3   Lose Kugelpackung.   Dichte  d = 0,0533  

k = 3   Lose Kugelpackung.   Dichte  d = 0,0447 

3.2.  2D-Netz (4, 6, 12) 

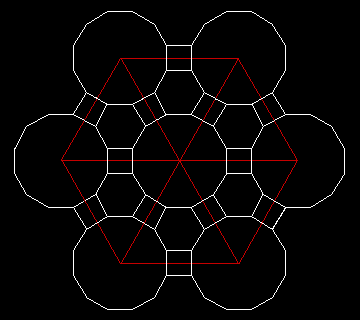
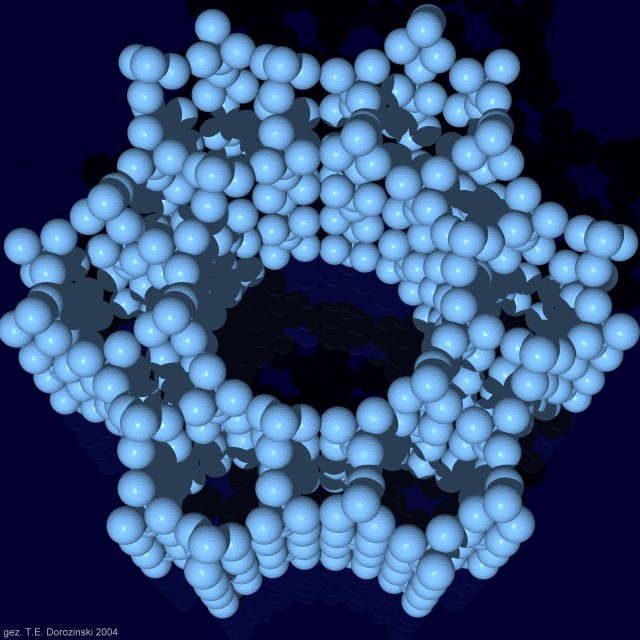
k = 4   Steife Kugelpackung.   Dichte d = 0,1031 

k = 3   Lose Kugelpackung.   Dichte  d = 0,0744

4. Lineare Kugelpackungen

Unter der Dichte d versteht man das Verhältnis des von Kugeln gefüllten Volumens zum Zylindervolumen.

Dichte  d = 2/3 = 0,667

Dichte  d = 0,472

Dichte  d = 0,5276

Dichte  d = 0,544

Dichte  d = 0,537

Dichte  d = 0,504   

Dichte  d = 0,376   

Ellipsoidpackungen (Beispiel)

k = 12   Dichte d = 0,6802   o2c-Objekt

Geschloßene Kugelpackung

Prof. Dr. Werner Fischer aus Marburg hat in seinen Publikation sehr viele Kugelpackungen untersucht und beschrieben.

Zurück

Kontakt

Startseite

Erstellt: im Dezember.2004;  Stand: 29.11.2023