
Geodätische Kuppeln (Sphären)
engl. Geodesic Domes
Kuppeln mit der Ikosaeder-Symmetrie:
Klasse I (Class I)
Klasse II (Class II)
Kuppeln ohne Symmetrieebenen, mit dem "Dreh" (twisted domes):
Klasse III (Class III)
NEU
Ein
anderer Weg geodätische Sphären zu generieren
Duale Kuppeln
Geosphären aus Drei-, Fünf- und Sechsecken
Abgestumpfte duale Kuppeln (truncated Goldberg polyhedra)
Hier die Formel um die Anzahl der Flächen in diesen Polyedern zu berechnen:
Die Anzahl der Dreiecke
F auf der ganzen Kuppel beträgt:
Fm,n = 30*(m² + mn + n²)
+ 2
wenn das Goldberg-Polyeder die Frequenz (m, n) hat.
Kuppeln mit anderen Symmetrien
1. Mit Tetraeder-Symmetrie

2. Mit Oktaeder-Symmetrie
3. Mit pyritoedrischer Symmetrie
4. Mit einer fünffachen Rotationsachse
Geosphären atypisch

Vielfalt der geodätischen Sphären - der Beitrag auf Geometryka
STEL-Files dazu:
Stel-1
Stel-2
Stel-3
Stel-4
Stel-5
Geodätische Kuppeln
sind
kugelförmige Gebilde, die
aus Dreiecken aufgebaut sind .
Die kleinste, "runde" Geosphäre ist das Ikosaeder, das aus 20 gleichseitigen Dreiecken
gebaut ist.
Das ist die beste Ausgangsfigur für weitere Geosphären.
Durch regelmäßiges Teilen in kleinere Dreiecke kann man Kuppeln mit größeren
Anzahl der Seitenflächen
konstruieren.
Im 2D-Dreiecksnetz kann man drei Netzpunkte so auswählen, dass ein gleichseitiges Dreieck gebildet wird (Abb.1).
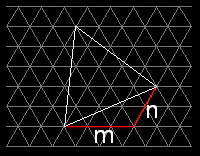 Abb.1
Abb.1  Abb.2
Abb.2
Dieses weiße Dreieck beinhaltet eine gewisse Anzahl von Netzmaschen (kleinen Dreiecken), wie es die Abb.2 zeigt.
Die Fläche der blauen Figur ist gleich wie die Fläche des weißen
Dreiecks.
Die Anzahl der kleinen Dreiecken in der blauen Figur kann man nach folgender Formel berechnen:
|
m=1 |
m=2 |
m=3 |
m=4 |
m=5 |
m=6 |
m=7 |
m=8 |
m=9 |
m=10 |
|
|
n=0 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
64 |
81 |
100 |
|
n=1 |
3 |
7 |
13 |
21 |
31 |
43 |
57 |
73 |
91 |
111 |
|
n=2 |
7 |
12 |
19 |
28 |
39 |
52 |
67 |
84 |
103 |
124 |
|
n=3 |
13 |
19 |
27 |
37 |
49 |
63 |
79 |
97 |
117 |
139 |
|
n=4 |
21 |
28 |
37 |
48 |
61 |
76 |
93 |
112 |
133 |
156 |
|
n=5 |
31 |
39 |
49 |
61 |
75 |
91 |
109 |
129 |
151 |
175 |
|
n=6 |
43 |
52 |
63 |
76 |
91 |
108 |
127 |
148 |
171 |
196 |
|
n=7 |
57 |
67 |
79 |
93 |
109 |
127 |
147 |
169 |
193 |
219 |
|
n=8 |
73 |
84 |
97 |
112 |
129 |
148 |
169 |
192 |
217 |
244 |
|
n=9 |
91 |
103 |
117 |
133 |
151 |
171 |
193 |
217 |
243 |
271 |
|
n=10 |
111 |
124 |
139 |
156 |
175 |
196 |
219 |
244 |
271 |
300 |
Im Beispiel der Abb.2 ist m=3 und n=2. N beträgt 19. Diese
19 Dreiecke projiziert man auf eine Seitenfläche des Ikosaeders, dann auf eine Kugel, und man hat ein Segment
der Kuppel. 20 Segmente bilden eine Geosphäre mit 20 * 19 = 380 Dreiecken.
Bei n=0 (Klasse I) und n=m (Klasse II) sind die Kuppeln symmetrisch, sonst haben wir zwei
chirale Formen: linke und rechte, spiegelbildlich gleich (Klasse III).
Eine bekannte geodätische Kuppel ist La Geode in Paris. Bei der ist m=20, n=0, F=8000, K=12000 und E=4002. Ihr Durchmesser beträgt 36 m.
© Tadeusz E.
Dorozinski
Kontakt
Erstellt:
Februar 2000
Stand 24.03.2025