Krzywe stożkowe

Metoda siatkowa wyznaczania punktów elipsy, paraboli i hiperboli

Krzywe stożkowe nie są łatwe do rysowania.
Przy pomocy metody siatkowej możemy stosunkowo prosto wyznaczyć dowolną ilość punktów na krzywych stożkowych. 
Metoda ta jest stosunkowo jednolita we wszystkich przypadkach, niezależnie jakie elementy krzywych są dane. Mogą to być osie lub średnice, wierzchołki, styczne i dowolne punkty.
Odpowiednie dwa odcinki dzielimy na równe cześci i z dwóch wierzchołków rysujemy pęki prostych. Punkty przecięcia dpowiednich par prostych wyznaczają punkty na krzywych stożkowych. 

Poniżej przedstawione są różne przypadki zastosowania tej metody.
Dane elementy zaznaczone są kolorem białym.

Metoda siatkowa wynika z pewnego przypadku ogólnego (patrz: Konrad Dyba "Perspektywa Linijna", WPWr 1979)

1. Elipsa

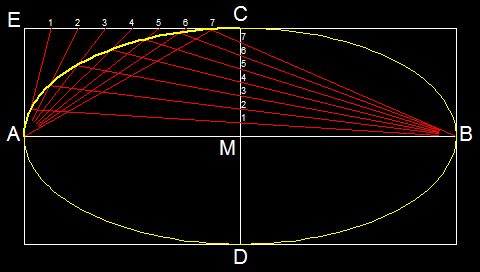
1.1  Dane są obie osie elipsy:

Abb. 1-1

1.2  Dana jest jedna para średnic sprzężonych:

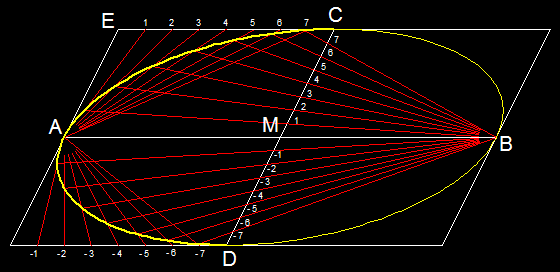
Abb. 1-2

1.3  Dana jest jedna średnica, kierunek drugiej średnicy sprzężonej i dowolny punkt elipsy:

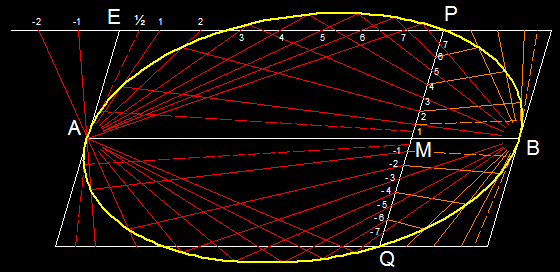
Abb. 1-3

2. Parabola

2.1  Dana jest oś lub średnica AB, przy czym punkt B jest punktem niewłaściwym, styczna w punkcie A i dowolny punkt C:

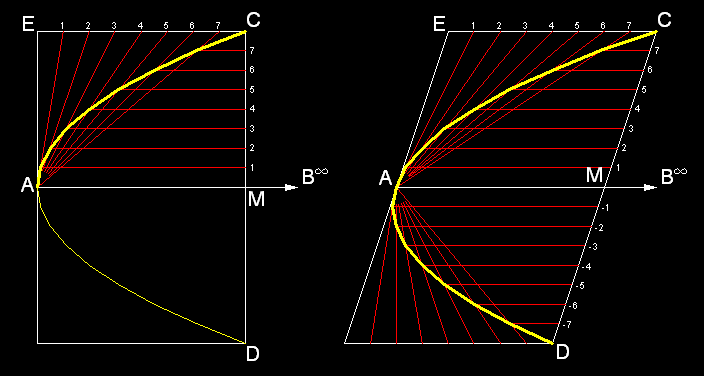
Abb. 2-1

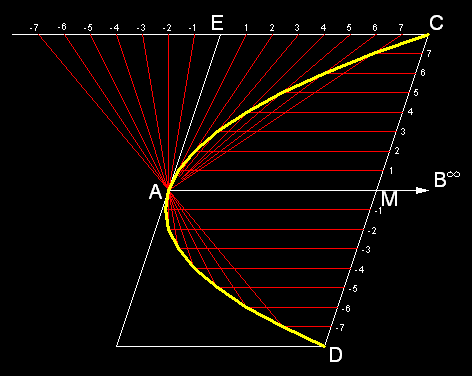
Abb. 2-2

3. Hiperbola

3.1  Dana jest oś lub średnica AB, styczna w punkcie A i dowolny punkt C:

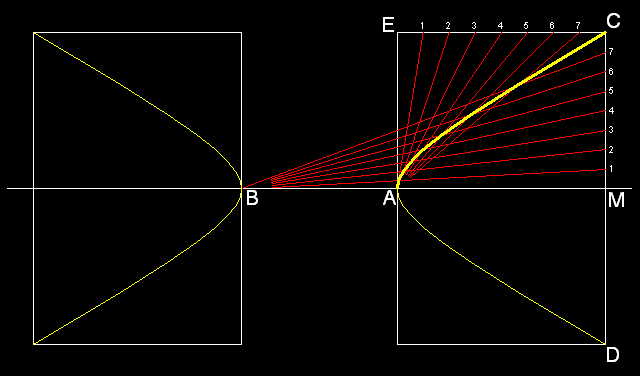
Abb. 3-1

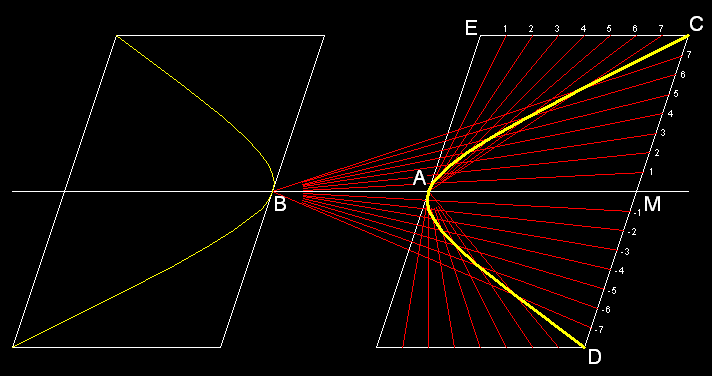
Abb. 3-2

Hiperbola ma dwie asymptoty. Tu można zobaczyć sposób ich wyznaczania.

_____________________________

Plik PDF:  Wierzchołek hiperboli, 

© Tadeusz E. Dorozinski

Kontakt

Stand: 20.03.2013

Startseite